[数论]Miller-Rabin素性测试

如果给出一个正奇数 n，要判断它是不是素数，有一个最简单暴力的方法，就是从 2 开始一直试到 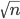，这样的话能保证结果绝对正确，但是，时间复杂度也就是 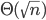，当 n 的规模到达 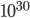甚至更高的级别的时候，就不能在可以忍受的时间内看到结果了。尤其是构造 RSA 密码体制时所需要用到的，找一个极大的素数。

那么，有没有一个比较快的方法来判断一个数是不是素数呢？

我们通过费马小定理知道，对于一个奇素数 p，有

那么对于一个奇数 p 来说，我们随机找一个 a，如果它满足上面那个式子的话，可以说 p 是素数吗？显然不行。

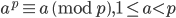
但是，如果它不满足上面那个式子，可以肯定它是合数，这是没问题的，而这个 a 就成为 p 的证据。

如果我们随机很多个数，发现这些数都满足上面的式子，那么我们可以认为 p 是一个可能的素数。

我们随机找一些合数，看看在 2～n 之间有多少个数是它们的证据

n	48	693	744	934
证据的数目	44	666	736	930
证据的百分比	0.917	0.961	0.989	0.996

一切看起来都不错，但是直到 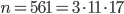的时候，你会发现它连一个证据都不存在！

这种数被称为 Carmichael 数，Carmichael 数的存在就说明我们要找一个更好的检验素数的方法，于是 Miller-Rabin 素性测试就诞生了。

还是一样的，如果一个数 p 是奇素数，那么记

设 a 是不被 p 整除的数，那么下面两个条件之一必然成立

• 
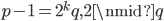
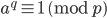
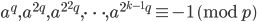• 之中有一个等式成立

根据如下命题

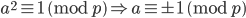
又因为上面第二个条件中的数，每一个都是前一个的平方，又因为最后一个数的平方是 1，所以往前，如果表中一个数它模 p 不余 1，但是它的平方模 p 余 1，那么那个数一定是 -1，所以在这种情况下表中包含 -1，又或者表中全是 1，那么第一个条件就会成立。

所以我们得到了 Miller-Rabin 素性测试的方法，也就是说，如果一个数不满足上面的性质，那么它就是和数，这个 a 就成为证据。而 Miller-Rabin 的证据和上面提到的方法的证据不同，它能够保证每一个奇合数 p 都会有不少于 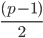个证据（具体证明还是看算法导论好了，似乎用了群论啥的）。

我们只要随机 50 个数来测试，那么测试失败的概率一定小于 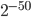，大约是 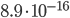，如果你觉得不够，还可以找更多的数来测试。

代码写起来实际上也不长，我写了一个 Javascript 版本的下面的按钮可以来玩哟（但是数不能太大 Javascript 没有啥高精库）！